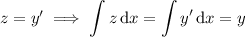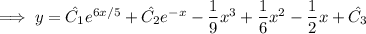Reduce the order of the ODE by setting
![z=y'[tex], so that [tex]z'=y''](https://img.qammunity.org/2018/formulas/mathematics/college/vc15esikoxm23zdsa3iedumk0cmgueb49t.png)
and
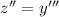
.
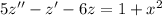
Consider the homogeneous ODE
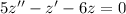
which has characteristic equation
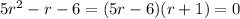
which has roots at
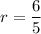
and
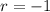
, so that the characteristic solution is
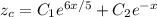
For the nonhomogeneous ODE,
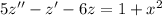
we can expect a particular solution of the form
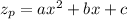
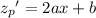
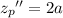
Substituting these expressions into the ODE yields
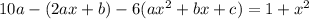
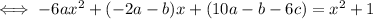
from which it follows that
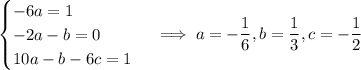
and so the particular solution is
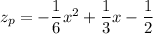
and the general solution for

is

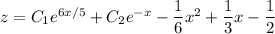
Integrate both sides once to solve for

: