Question

Given the position of the particle, when is the particle at rest

Answer 1

`s(t)=(2)/(3)t^3-(9)/(2)t^2-18t`

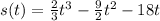
To find when the particle is at rest, equal the velocity function (derivate of the position function) to 0 and solve t:

Velocity function:

`\begin{gathered} v(t)=\frac{d}{\text{ d t}}((2)/(3)t^3-(9)/(2)t^2-18t) \\ \\ v(t)=(2)/(3)(3t^2)-(9)/(2)(2t)-18(1) \\ \\ v(t)=2t^2-9t-18 \end{gathered}`

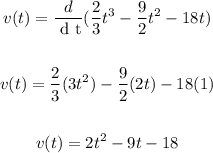
Equal to 0 the equation above:

`2t^2-9t-18=0`

Solve t:

`\begin{gathered} \text{Factor:} \\ 2t^2+3t-12t-18=0 \\ t(2t+3)-6(2t+3)=0 \\ (t-6)(2t+3)=0 \\ \\ t-6=0 \\ t=6 \\ \\ 2t+3=0 \\ 2t=-3 \\ t=-(3)/(2) \end{gathered}`

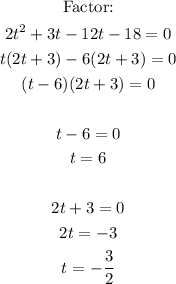
Solutions for t are: t=6 and t=-3/2.

As the time cannot be a negaive amount. The particle is at rest at a time of 6