Answer:
$45950.57
Explanation:
We have been given that the Laffite family deposits $8500 in a savings account at 6.75% interest, compounded continuously.
To find the amount in the account after 25 years we will use continuous compounded interest formula.
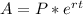 ,where,
,where,
A = Final amount after t years,
P = Principal amount,
e = Mathematical constant,
r = Interest rate in decimal form,
t = Time.
Let us convert our given rate in decimal form.
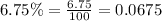
Upon substituting our given values in above formula we will get,
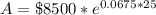
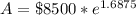
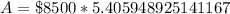
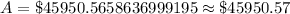
Therefore, there will be $45950.57 in the account after 25 years.