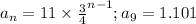Question

Given the functions f(n) = 11 and g(n) = (three fourths)n − 1, combine them to create a geometric sequence, an, and solve for the 9th term.

an = (11 • three fourths)n − 1; a9 ≈ 24.301
an = 11(three fourths)n − 1; a9 ≈ 1.101
an = 11 + (three fourths)n − 1; a9 ≈ 11.100
an = 11 − (three fourths)n − 1; a9 ≈ 9.900

Answer 1

We are given two functions:
f(n) = 11
g(n) = (3/4) ^(n-1)
I have rewritten the functions to their correct form. Notice that the term (n - 1) is the exponent of 3/4.

We are asked to combine the two functions to model a geometric sequence and solve for the 9th term.

The general formula for a geometric sequence is
an = a1 r^(n - 1)

From the given functions, we can set
f(n) = a1 = 11
and
g(n) = r^(n - 1) = (3/4)^(n - 1)

Substituting to the general formula of a geometric sequence, the result is
an = 11 (3/4)^(n - 1)

Solving for the 9th term
a9 = 11 (3/4)^(9 - 1)
a9 = 1.101

The answer is the second option.

Answer 2

Option 2

`a_n=11* (3)/(4)^(n-1); a_9=1.101`

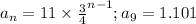
Explanation:

Given : The functions
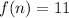`f(n) = 11` and
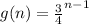`g(n) = (3)/(4)^(n-1)` combine them to create a geometric sequence, an

To find : The 9th term

Solution :

The two function are :

`f(n) = 11`

`g(n) = (3)/(4)^(n-1)`

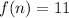
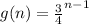
We have to form a geometric sequence by combining f(n) and g(n).

So, the sequence having nth term is

`a_n=f(n)* g(n)`

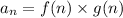
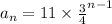`a_n=11* (3)/(4)^(n-1)` ........[1]

Now, we put n=1,2,3,... to make a sequence

Put n=1 in [1]

`a_2=11* (3)/(4)^(2-1)`

`a_2=11* (3)/(4)`

`\text{Common ratio}=\frac{\text{Second Term}}{\text{First Term}}`

`r=(a_2)/(a_1)`

`r=(11* (3)/(4))/(11)`

`r=(3)/(4)`

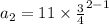
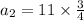
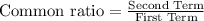
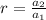
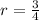
The formula of nth term in geometric sequence is

`T_n=a_1* r^(n-1)`

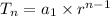
Put n= 9 to find 9th term

`T_9=11* (3)/(4)^(9-1)`

`T_9=11* (3)/(4)^(8)`

`T_9=11* 0.1001`

`T_9=1.101`

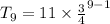
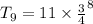
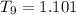
Therefore, Option 2 is correct.

`a_n=11* (3)/(4)^(n-1); a_9=1.101`