Question

1) Find all the zeros of the function: g(x)= x^3+3x^2-18x-40, given that one factor is (x+5) 2)Find all zeros of the function: g(x)= x^3+x^2-17x+15, given that one zero is x=1

Answer 1

It is given that

`g(x)=x^3+3x^2-18x-40`

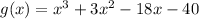
The one factor of g(x) is (x+5).

By using the synthetic method, we get

`g(x)=(x+5)(x^2-2x-8)`

`g(x)=(x+5)(x^2-4x+2x-8)`

`g(x)=(x+5)(x(x-4)+2(x-4))`

`g(x)=(x+5)(x-4)(x+2)`

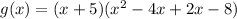
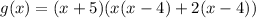
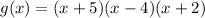
Hecne zeros of g(x) is -5,4, and -2.

2)

It is given that

`g(x)=x^3+x^2-17x+15`

The one zero of the given g(x) is x=1.

By using the synthetic method, we get

`g(x)=(x-1)(x^2+2x-15)`

`g(x)=(x-1)(x^2+3x-5x-15)`

`g(x)=(x-1)(x(x+3)-5(x+3))`

`g(x)=(x-1)(x+3)(x-5)`

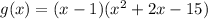
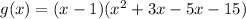
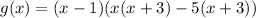
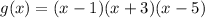
To find zeros of g(x) by equating g(x) to zero.

`g(x)=(x-1)(x+3)(x-5)=0`

`(x-1)=0;(x+3)=0;(x-5)=0`

`x=1;x=-3;\text{ x=5}`

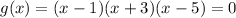
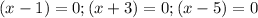
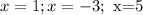
Hence the zeros of the given function g(x) are 1,-3, and 5.