Question

What is the solution to the equation y/y-4-4/y+4=32/y^2-16

Answer 1

Explanation:

The answer is NO SOLUTION

Answer 2

ANSWER

No solution


EXPLANATION


`(y)/(y - 4) + (y)/(y - 4) = \frac{32}{ {y}^(2) - 16}`


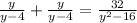
The least common multiple is

`{y}^(2) - 16 = (y - 4)(y + 4)`


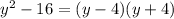
We multiply through by the LCM to obtain,





`(y - 4)(y + 4) * (y)/(y - 4) + (y - 4)(y + 4) * (y)/(y - 4) = \frac{32}{ {y}^(2) - 16} * (y - 4)(y + 4)`


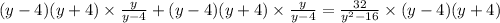
We cancel out to get,


`y(y + 4) + y(y - 4) = 32`


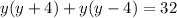
We expand to get,



`{y}^(2) + 4y + {y}^(2) - 4y = 32`


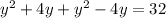
We now group like terms to obtain,



`{y}^(2) + {y}^(2) + 4y - 4y = 32`


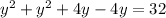
We simplify to get,


`2 {y}^(2) + 0 = 32`



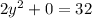
This gives,


`2 {y}^(2) = 32`


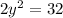
We divide through by 2.



`y ^(2) = 16`


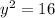
Taking square root of both sides gives,


`y = \pm √(16)`



`y = \pm4`


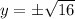
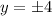
This implies that,



`y = 4 \: or \: y = - 4`



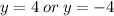
But the above solutions are not within the domain of the function, which is


`y \\e4 \: or \: y \\e - 4`


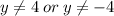
Therefore the equation has no solution.