Question

Continuous differentiable?

The figure shows two parts of the graph of a continuous differentiable function
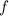
`#f#` on [-10,4].
The derivative
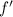
`#f'#` is also continuous.

(a) Explain why
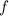
`#f#` must have at least one zero in [-10,4].

(b) Explain why
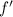
`#f'#` must also have at least one zero in the interval [-10,4]. What are these zeros called?

(c) Make a possible sketch of the function with one zero of
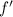
`#f'#` on the interval [-10,4]

Answer 1

a)
Since in the given range the function is continuous and has arguments for which it's greater than zero and less than zero, then the graph of the function must intersect the x-axis, meaning there's at least one zero.

b)
In the part of the graph on the left the function is increasing and on the part on the right it's decreasing. That means there is an extremum (maximum). And where the extremum is, the derivative is equal to 0.

c)
attachment