Question

Find the 12th term of the sequence which has a first term of 14 and has a common ratio of 1.03

Answer 1

A(n)=a × r^n-1
A(12)= 14 x 1.03^11
A(12)=19.379

Answer 2

`S_(12) = 19.376`.

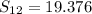Explanation:

Given : sequence which has a first term of 14 and has a common ratio of 1.03.

To find :Find the 12th term of the sequence .

Solution : We have given first term of 14 and has a common ratio of 1.03.

Sum of n terms (
`S_(n) = a r^(n-1)`.

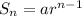Where, a = first term , r = common ratio and n = number of terms .

Then, Plug the values a = 14 , r = 1.03 , n = 12.

`S_(12) = 14 (1.03)^(12-1)`.

`S_(12) = 14 (1.03)^(11)`.

`S_(12) = 14 ( 1.384)`.

`S_(12) =19.376`.

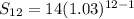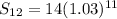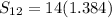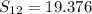Therefore,
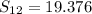`S_(12) = 19.376`.