Answer: The length of AB is 48 units.
Step-by-step explanation: As shown in the attached figure below, ABC is a right-angled triangle where ∠B = 90°, AC = 96 cm and ∠C = 30°.
We are to find the length of side AB.
We know that
the sine of an acute angle in a right-angled triangle is the ratio of the perpendicular to hypotenuse of the triangle.
For angle C, the perpendicular is AB and hypotenuse is AC, the side opposite to the right angle.
Therefore, we get
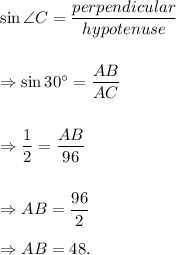
Thus, the length of AB is 48 units.