Answer:
Yes
Explanation:
If you have a line, for example:
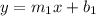
where
 is the slope and
is the slope and
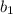 is the point where that line crosses the y axis calles the y-intercept.
is the point where that line crosses the y axis calles the y-intercept.
And another line parallel to the first line:
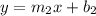
the slopes of both lines must meet the following condition
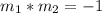
so as we can see we have a condition for the slope of a parallel line, but we dont have a condition or restriction for the y-intercept of the parallel line, so
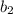 can have any value (an infinite number of values)
can have any value (an infinite number of values)
which means that there are an infinite number of parallel lines for any straight line.