Question

X4 − 4x3 = 6x2 − 12x From least to greatest, what are the integral roots of the equation?

The answer is -2 and 0. I had to take an L.

Answer 1

The integral roots of the equation are 0 and -2.

Explanation:

Here, the given equation,

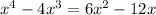
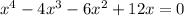
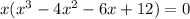`x^4 - 4x^3 = 6x^2 - 12x`

`x^4-4x^3-6x^2+12x=0`

`x(x^3-4x^2-6x+12)=0` ------(1),

Since,
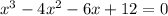`x^3-4x^2-6x+12=0` at x = - 2,

Thus, x + 2 is a factor of
`x^3-4x^2-6x+12=0`,

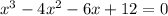By dividing
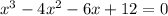`x^3-4x^2-6x+12=0` by (x+2),

We get,
`x^2-6x+6`

Hence,

`x^3-4x^2-6x+12=(x+2)(x^2-6x+6)`

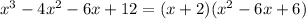
By equation (1),

`x(x^3-4x^2-6x+12)=x(x+2)(x^2-6x+6)`

`\implies x(x+2)(x^2-6x+6)=0`

`\implies x(x+2)(x-(3+√(3)))(x-(3-√(3)))=0`

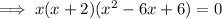
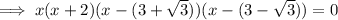
If x + 2 = 0 ⇒ x = -2,

While, if x - (3 ± √3 ) = 0 ⇒ x = 3 ± √ 3

Thus the roots of the given equation are, x = 0, - 2, 3 ± √3,

Since, 0 and - 2 are integers,

⇒ The integral roots of the equation are 0 and -2.

Answer 2

The integral roots are -2, 0.

Solution-

The given polynomial is,

`x^4-4x^3-6x^2+12x`

For calculating the roots,

`\Rightarrow x^4-4x^3-6x^2+12x=0`

`\Rightarrow x(x^3-4x^2-6x+12)=0`

Decomposing the terms,

`\Rightarrow x(x^3-6x^2+2x^2+6x-12x+12)=0`

Rearranging the terms,

`\Rightarrow x(x^3-6x^2+6x+2x^2-12x+12)=0`

`\Rightarrow x[x(x^2-6x+6)+2(x^2-6x+6)]=0`

`\Rightarrow x[(x+2)(x^2-6x+6)]=0`

`\Rightarrow x(x+2)(x^2-6x+6)=0`

`\Rightarrow x=0,\ x=-2,\ x=(-(-6)\pm √((-6)^2-4\cdot 1\cdot 6))/(2\cdot 1)`

`\Rightarrow x=0,\ x=-2,\ x=(6\pm √(12))/(2)`

`\Rightarrow x=0,\ x=-2,\ x=3\pm √(3)`

Therefore, the integral roots are -2, 0.