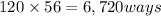Answer:
The committee could be made in 6,720 ways
Step-by-step explanation:
Parameters:
• Total number of teachers avalable = 8
• Number of teachers to be chosen from this = 5
• Total number of students = 10
• Number of students to be chosen from this = 3
We have number of ways for each group to be:
Teachers:
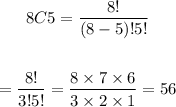
Students:
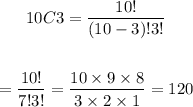
Finally, the committee could be made in