Question

9. Which pair of equations below represent perpendicular lines?

A) Y = 7/8x + 12 and y = -8/7x – 8
B) Y = 5x + 15 and y = -5x + 15
C) Y = 4x + 9 and y = 4x -9
D) Y = 9 and y = 18

Answer 1

A is correct. ...................................................

Answer 2

`y =(7)/(8)x + 12` and
`y = -(8)/(7)x - 8`

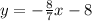
Explanation:

The product of the slopes of the perpendicular lines is -1

Option 1)
`y =(7)/(8)x + 12` and
`y = -(8)/(7)x - 8`

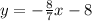
General equation of line :
`y=mx+c`

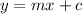
Comparing with general equation

Slope of line 1 =
`(7)/(8)`

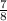
Slope of line 2=
`-(8)/(7)`

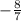
Now product of slopes =
`(7)/(8) * (-8)/(7)`

=
`-1`

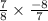
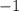
Since The product of the slopes of the perpendicular lines is -1

So,
`y =(7)/(8)x + 12` and
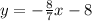`y = -(8)/(7)x - 8` represent perpendicular lines

Option 2)
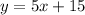`y = 5x + 15` and
`y = -5x + 15`

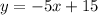
General equation of line :
`y=mx+c`

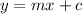
Comparing with general equation

Slope of line 1 = 5

Slope of line 2= -5

Now product of slopes =
`5 * -5`

=
`-25`

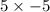
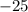
Since The product of the slopes of the perpendicular lines is not -1

So,
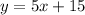`y = 5x + 15` and
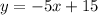`y = -5x + 15` does not represents the perpendicular lines.

Option 3)
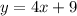`y = 4x + 9` and
`y = 4x -9`

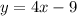
General equation of line :
`y=mx+c`

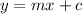
Comparing with general equation

Slope of line 1 = 4

Slope of line 2= 4

Now product of slopes =
`4 * 4`

=
`16`

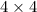
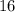
Since The product of the slopes of the perpendicular lines is not -1

So,
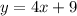`y = 4x + 9` and
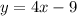`y = 4x -9`does not represents the perpendicular lines.

Option 4)
`y = 9` and
`y = 18`

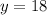
General equation of line :
`y=mx+c`

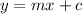
Comparing with general equation

Slope of line 1 = 0

Slope of line 2=0

Now product of slopes =
`0 * 0`

=
`0`

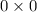
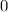
Since The product of the slopes of the perpendicular lines is not -1

So,
`y = 9` and
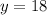`y = 18` does not represents the perpendicular lines.