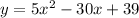2 Answers

Ravi Soni · Answer 1 · 2018-06-26T18:31:59+0000

Answer:

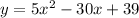
$y = 5x{^2} - 30x + 39$

Explanation:

Given the vertex form of the equation of a parabola to be
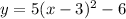
y = 5(x-3)^(2) - 6

The standard form of the equation will be a quadratic equation in the form;

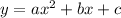
y = ax^(2) + bx + c

where,

y is dependent variable

x is independent variable

a and b are constant coefficients of independent variable x² and x respectively

c is a constant

Transforming the vertex form to the standard form of a quadratic function y, we develop the equation:

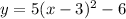
y = 5(x-3)^(2) - 6

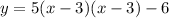
y = 5(x-3)(x-3) - 6

y = 5(x^(2) - 6x + 9) - 6

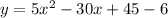
$y = 5x{^2} - 30x + 45 - 6$

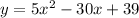
$y = 5x{^2} - 30x + 39$

The standard form of the equation is
$y = 5x{^2} - 30x + 39$

Please log in or register to add a comment.