Question

For a given velocity of projection in a projectile motion, the maximum horizontal distance is possible only at ө = 45°. Substantiate your answer with mathematical support.

Answer 1

Consider the projectile launched at initial velocity V at angle θ relative to the horizontal.
Neglect wind or aerodynamic resistance.

The initial vertical velocity is Vsinθ.
When the projectile reaches its maximum height of h, its vertical velocity will be zero.
If the time taken to attain maximum height is t, then
0 = Vsinθ - gt
t = (Vsinθ)/g, where g = acceleration due to gravity.

The horizontal component of launch velocity is Vcosθ. This velocity remains constant because aerodynamic resistance is ignored.
The time to travel the horizontal distance D is twice the value of t.
Therefore
D = Vcosθ*[(2Vsinθ)/g]
= (2V²sinθ cosθ)/g
= (V²sin2θ)/g

In order for D (horizontal distance) to be maximum,
`image`
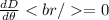
That is,

`(2V^(2))/(g) cos(2 \theta )=0`

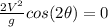
Because
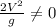
`(2V^(2))/(g) \\eq 0`, therefore cos(2θ) = 0.
This is true when 2θ = π/2 => θ = π/4.

It has been shown that the maximum horizontal traveled can be attained when the launch angle is π/4 radians, or 45°.