Answer:
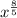 .
.
Explanation:
We are asked to find the simplified form of expression: The fifth root of x to the fourth power times the fifth root of x to the fourth power.
First of all we will write an expression from our given information as:
![\sqrt[5]{x^4}* \sqrt[5]{x^4}](https://img.qammunity.org/2018/formulas/mathematics/high-school/f5vgksnrco4l47v55wj8wu05m58t4i3u3i.png)
Using exponent property for radicals
![\sqrt[n]{a^m}=a^{(m)/(n)}](https://img.qammunity.org/2018/formulas/mathematics/middle-school/fqxowpe1qxyw0fqsg4njj10tmu1xuws095.png) , we can rewrite our expression as:
, we can rewrite our expression as:
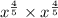
Using exponent property
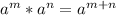 , we can rewrite our expression as:
, we can rewrite our expression as:
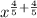
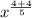
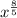
Therefore, the simplified form of our given expression would be
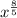 .
.