Question

Find the inverse of the function.

f(x) = x3 - 8

Answer 1

To find the inverse all you do is switch the x and y and rewrite the equation.

So if our original equation is y = x^3 - 8, then switch the x and y

x = y^3 - 8 .... and now solve for y

x + 8 = y^3

y = cube root (x + 8), or you can write it as y = (x + 8)^ (1/3)

Answer 2

`f^(-1)(x)=\sqrt[3]{x+8}`

Explanation:

`f(x) = x^3 - 8`

To get inverse function , follow the steps

Replace f(x) by y

`y = x^3 - 8`

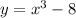
Swap the variables x and y. Replace x with y and y with x

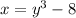`x= y^3 - 8`, solve the equation for y

Add 8 on both sides

`x+8= y^3`

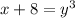
To remove cube , take cube root on both sides

`\sqrt[3]{x+8} =y`

Now replace y with f inverse

`\sqrt[3]{x+8} =f^(-1)(x)`