Question

What are the domain and range of f(x) = 2(3^x)?

domain: (-infinity, infinity); range: (0, infinity)
domain: (-infinity, infinity); range: (2,infinity)
domain: (0, infinity); range: (-infinity, infinity)
domain: (2,infinity); range: (-infinity, infinity)

Answer 1

Okay so the domain in this example is -infinity to infinity because 3^x is never an illegal expression where x is any number. As you decrease the value of the domain, 3^x approaches 0, we can assume that it eventually reaches 0, since 2 multiplied by 0 is still 0, the range must be (0, infinity).

Therefore, the answer is the first one.

Answer 2

domain: (-infinity, infinity); range: (0, infinity)

Explanation:

The domain of a function are the values that the variable x takes.

In this case x can take any value, that is, the domain of the function is (-infinity, infinity).

The range of a function are the values that the function itself takes, f (x).

In this case, being a negative exponential, as the values of x become smaller, the function tends to 0, and if the values are larger the function tends to infinity, therefore the range of the function is (0 , infinite).

For example:

When x = -300,000

`f(-300,000)=2(3^(300,000))=0`

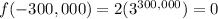
When x = 100

`f(100)=2(3^(100))=1*10^(48)`

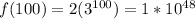
So, the answer is :

domain: (-infinity, infinity); range: (0, infinity)