Question

The stopping distance, d ( in feet) for a truck moving at a velocity (speed) v miles per hour is modeled by the equation: d=0.04v^2+1.1v What is the speed of the truck if it takes 100 feet to stop? a. 12.5 mph c. 18 mph b. 38 mph d. 13 mph

Answer 1

its b-38 just took it

Answer 2

b. 38 mph

Explanation:

Here, the given equation that shows the stopping distance ( in feet ) when the truck is moving with the speed of v miles per hour,

`d=0.04v^2+1.1v`

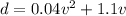
If d = 100,

`100=0.04v^2+1.1v`

`\implies 0.04v^2+1.1v=100`

`0.04(v^2+(1.1)/(0.04))=100`

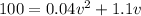
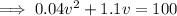
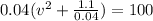
By adding the square of the half of the coefficient of v on both sides,

We get,

`0.04(v+13.75)^2=107.563`

`v+13.75=\pm √(107.563)`

`v=-13.75 \pm √(107.563)`

`\implies v=-13.75-√(107.563)\text{ or } v = 13.75+√(107.563)`

`\implies v\approx 38.1063\text{ or } v\approx -65.6063`

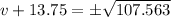
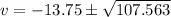
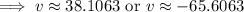
Since, the speed can not be negative,

Hence, the approximate speed of truck would be 38 mph.

Option 'b' is correct.