Question

The table below shows the radius y, in inches, created by growing algae in x days: Time (x) (days) 1 4 7 10 Radius (y) (inches) 1 8 11 12 Part A: What is the most likely value of the correlation coefficient of the data in the table? Based on the correlation coefficient, describe the relationship between time and radius of the algae. [Choose the value of the correlation coefficient from 1, 0.94, 0.5, 0.02.] (4 points) Part B: What is the value of the slope of the graph of radius versus time between 4 and 7 days, and what does the slope represent? (3 points) Part C: Does the data in the table represent correlation or causation? Explain your answer. (3 points)

Answer 1

PART A:
Given the table below showing the radius y, in inches, created by growing algae in x days.

Time (x) (days): 1 4 7 10
Radius (y) (inches): 1 8 11 12

We can find the find the correlation coeficient of the data using the table below:

`\begin{center} \begin{tabular} c x & y & x^2 & y^2 & xy \\ [1ex] 1 & 1 & 1 & 1 & 1\\ 4 & 8 & 16 & 64 & 32\\ 7 & 11 & 49 & 121 & 77\\ 10 & 12 & 100 & 144 & 120\\ [1ex] \Sigma x=22 & \Sigma y=32 & \Sigma x^2=166 & \Sigma y^2=330 & \Sigma xy=230 \end{tabular} \end{center}`

Recall that the correlation coefitient is given by the equation:

`r= (n(\Sigma xy)-(\Sigma x)(\Sigma y))/( √((n\Sigma x^2-(\Sigma x)^2)(n\Sigma y^2-(\Sigma y)^2)) ) \\ \\ = (4(230)-(22)(32))/( √((4(166)-(22)^2)(4(330)-(32)^2)) ) = (920-704)/( √((664-484)(1,320-1,024))) \\ \\ = (216)/( √(180(296))) = (216)/( √(53,280) ) = (216)/(230.8) =0.94`

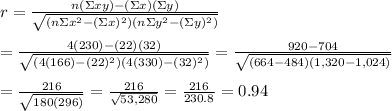
[Notice: even without using the formular to find the value of the correlation coeficient, it can be seen that the value of y strictly increases as the valu of x increases. This means that the value of the correlation coeficient is closer to +1 and from the options the value that is closest to +1 is 0.94]

From the value of the correlation coeffeicient, it can be deduced that the radius of the algae has a strong positive relationship with the time.

Recall the for the value of the correlation coeficient closer to +1, the relationship is strong positive, for the value closer to -1, the value is strong negative and for the values closer to zero, either way of zero is a weak positive if it is positive and weak negative if it is negative.


PART B:
Recall that the slope of a straight line passing through two points

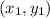
`(x_1,y_1)` and
`(x_2,y_2)`
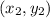
is given by

`m= (y_2-y_1)/(x_2-x_1)`

Thus the slope of the graph of radius versus time between 4 and 7 days, [i.e. the line passes through points (4, 8) and (7, 11)] is given by

`m= (11-8)/(7-4)= (3)/(3) =1`

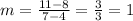
The value of the slope means that the radius of the algea grows by 1 inch evry day between day 4 and day 7.


PART C:
We can say that the data above represent both correlation and causationg.

Recall that correlation expresses the relationship between two variables while causation expresses that an event is as a result of another event.

From the information above, we have seen that there is a relationship (correlation) between the passing of days and the growth in the radius of the algae.

Also we can conclude that the growth in the radius of algae is a function of the passing of days, i.e. the growth in the radius of algae is as a result of the passing of days.

Therefore, the data in the table represent both correlation and causation.