Question

​Recently, More Money 4U offered an annuity that pays 5.7 % compounded monthly. If $1,011 is deposited into this annuity every​ month, how much is in the account after 6​years? (Round to the nearest dollar) Part 2 of the question: How much of this is​ interest? (Round to the nearest dollar)

Answer 1

Recall that the future value (FV), of an annuity payment of $P, for, n years at, t times a year at, r% interest compounded, t times a year is given by

`FV=P (\left(1+ (r)/(t) \right)^(nt)-1)/((r)/(t))`

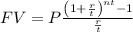
Given that More Money 4U offered an annuity that pays r = 5.7% = 0.057 compounded monthly (12 times a year or t = 12). If P = $1,011 is deposited into this annuity every​ month (t = 12), then after n = 6 years the amount in the account is given by:

`FV=1,011* (\left(1+ (0.057)/(12) \right)^(6*12)-1)/((0.057)/(12)) \\ \\ =1,011* ((1+0.00475)^(72)-1)/(0.00475) =1,011* ((1.00475)^(72)-1)/(0.00475) \\ \\ =1,011* (1.406621-1)/(0.00475) =1,011* (0.406621)/(0.00475) =1,011*85.6044 \\ \\ =\$86,546.05`

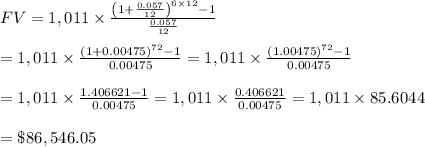
Therefore, the amount in the account after 6​years rounded to the nearest dollar is $86,546.


PART 2:
Given that $1,011 is deposited into this annuity every​ month for 6 years, the amount deposited into the account is given by
$1,011 x 12 x 6 = $72,792

Therefore, the amount of interest accrued is given by
$86,546 - $72,792 = $13,754

Therefore, the amount of interest received is $13,754