Question

Find the linear approximation of the data that passes through the points 5,3 and 20,6

Answer 1

namely, the equation of that line with those points





`\bf y-{{ y_1}}={{ m}}(x-{{ x_1}})\qquad \begin{array}{llll} \textit{plug in the values for } \begin{cases} y_1=3\\ x_1=5\\ m=\boxed{?} \end{cases}\\ \textit{and solve for`

Answer 2

`y=(1)/(5)(x)+2`

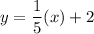
Explanation:

The linear approximation of the data that passes through the points (5,3) and (20,6).

We need to find the equation of line.

If a line passes through two points, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

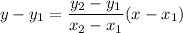
The line passes through (5,3) and (20,6). So, the equation of line is

`y-3=(6-3)/(20-5)(x-5)`

`y-3=(3)/(15)(x-5)`

`y-3=(1)/(5)(x-5)`

`y-3=(1)/(5)(x)-(1)/(5)(5)`

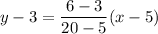
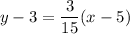
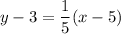
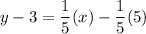
Add 3 on both sides.

`y=(1)/(5)(x)-1+3`

`y=(1)/(5)(x)+2`

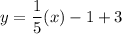
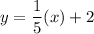
Therefore, the equation of linear approximation is
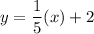`y=(1)/(5)(x)+2`.