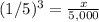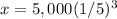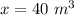Question

The scale factor of a model of a hot air balloon to the actual hot air balloon is 1 to 5. the volume of the actual balloon is 5000 m^3 what is the volume ? A. 0.005 m^3 B.0.025 m^3 C. 40 m^3 D.200 m^3

Answer 1

`\bf \qquad \qquad \textit{ratio relations} \\\\ \begin{array}{ccccllll} &Sides&Area&Volume\\ &-----&-----&-----\\ \cfrac{\textit{similar shape}}{\textit{similar shape}}&\cfrac{s}{s}&\cfrac{s^2}{s^2}&\cfrac{s^3}{s^3} \end{array} \\\\ -----------------------------\\\\ \cfrac{\textit{similar shape}}{\textit{similar shape}}\qquad \cfrac{s}{s}=\cfrac{√(s^2)}{√(s^2)}=\cfrac{\sqrt[3]{s^3}}{\sqrt[3]{s^3}}\\\\ -------------------------------\\\\`


`\bf \cfrac{model}{actual}\qquad \cfrac{s}{s}=\cfrac{\sqrt[3]{s^3}}{\sqrt[3]{s^3}}\implies \cfrac{1}{5}=\cfrac{\sqrt[3]{v}}{\sqrt[3]{5000}}\implies \cfrac{1}{5}=\sqrt[3]{\cfrac{v}{5000}} \\\\\\ \left( \cfrac{1}{5} \right)^3=\cfrac{v}{5000}\implies \cfrac{1^3}{5^3}=\cfrac{v}{5000}\implies \cfrac{1}{125}=\cfrac{v}{5000}`

solve for "v"

Answer 2

Option C

`40\ m^(3)`

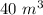
Explanation:

Let

x-------> the volume of the model

y------> he volume of the actual

z------> the scale factor

we know that

The scale factor elevated to the cube is equal to the volume of the model divided by the volume of the actual

so

`z^(3)=(x)/(y)`

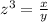
we have

`z=1/5, y=5,000\ m^(3)`

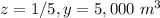
substitute and solve for x

`(1/5)^(3)=(x)/(5,000)`

`x=5,000(1/5)^(3)`

`x=40\ m^(3)`