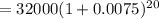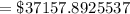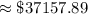Question

A certificate of deposit earns 0.75% interest every three months. The interest is compounded. What is the value of a $32,000 investment after 5 years?

$32,426.67

$37,157.89

$43,099.36

$57,795.56

Answer 1

`\bf \qquad \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\to &\$32000\\ r=rate\to 0.75\%\to (0.75)/(100)\to &0.0075\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{every 3months, or quarter} \end{array}\to &4\\ t=years\to &5 \end{cases} \\\\\\ A=32000\left(1+(0.0075)/(4)\right)^(4\cdot 5)`

Answer 2

$ 37,157.89

Explanation:

Given,

The initial deposit, P = $ 32,000,

Which earns 0.75% compound interest every three months.

Thus, the rate per three months, r = 0.75 % = 0.0075.

Time = 5 years,

So, the number of periods ( of three months ) in 5 years, n = 20

( 1 year = 12 months ⇒ The number of three month period in 1 year = 4 )

Thus, the amount after 5 years,

`A=P(1+r)^n`

`=32000(1+0.0075)^(20)`

`=\$ 37157.8925537`

`\approx \$ 37157.89`