Question

A theme park guest takes an innertube into the wave pool. The innertube moves up and down in a way such that the height h of the innertube, in meters, above the floor of the pool can be modeled by the function h = asinbx + 5. When the wave pool is turned on, the innertube's height fluctuates between 2 meters and 8 meters, with an interval of 12 seconds between maximums. Based on the context of the problem, what are the values of a and b?

Answer 1

So we are told that the height of the innertube in meters is given by:

`h(x)=a\sin (bx)+5`

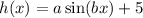
The minimum height is 2 meters, the maximum is 8 meters and the time between two consecutive maximums is 12 seconds. Here is important to note a few properties of the sine. First of all, the minimum value of sin(bx) is -1 and its maximum value is 1. Then the height of the innertube is minimum when sin(bx)=-1 and maximum when sin(bx)=1. With these two values we can build two equations for a:

`\begin{gathered} \min (h)=2=a\cdot(-1)+5 \\ \max (h)=8=a\cdot1+5 \end{gathered}`

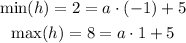
So we have:

`\begin{gathered} 2=-a+5 \\ 8=a+5 \end{gathered}`

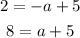
Substracting 5 from both sides of the second equation we get:

`\begin{gathered} 8-5=a+5-5 \\ 3=a \end{gathered}`

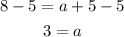
Using this in the first equation gives us:

`\begin{gathered} 2=-3+5 \\ 2=2 \end{gathered}`

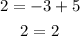
Which confirms that a=3. Now we have to find b. For this purpose we can recal another property of the sine. Its period i.e. the distance (in this case the time) between two consecutive maximums is given by:

`(2\pi)/(b)`

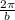
Since we know this time is 12 seconds we get:

`(2\pi)/(b)=12`

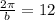
If we multiply both sides by b and divide them by 12 we get:

`\begin{gathered} (2\pi)/(b)\cdot(b)/(12)=12\cdot(b)/(12) \\ (2)/(12)\pi=b \\ (\pi)/(6)=b \end{gathered}`

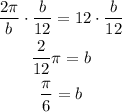
So we have:

`a=3\text{ and }b=(\pi)/(6)`

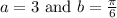
Which means that the answer is the second option.