Question

The impulse given to a ball with mass of 2.0 kg is 16 N*s. If the ball were already moving at 3.0 m/s., what would the final velocity be? (Remember that v = Vfinal - Vinitial ) 5 m/s 11 m/s 29 m/s 35 m/s

Answer 1

11 m/s

Step-by-step explanation:

The impulse given to the ball is equal to its change in momentum:

`I=\Delta p=m \Delta v= m(v_f -v_i)`

where

m=2.0 kg is the mass of the ball

`v_i=3.0 m/s` is the initial velocity of the ball

`v_f` is the final velocity of the ball

`I=16 Ns` is the impulse

If we re-arrange the formula and we replace the numbers, we can find the final velocity:

`v_f = (I)/(m)+v_i=(16 Ns)/(2.0 kg)+3.0 m/s=11 m/s`

Answer 2

The correct answer to the question is 11 m/s.

CALCULATION:

The mass of the ball is given as m = 2.0 kg.

The impulse exerted on the ball is 16 N-s.

The initial velocity of the ball u = 3 m/s.

We are asked to calculate the final velocity v.

The impulse of a ball is defined as the product of force with time. On the other hand, it can be defined as the change in momentum of a body.

Mathematically it can be written as -

Impulse = mv - mu = dp.

Here, p stands for the momentum.

From above we see that impulse = 16 N-s.

⇒ mv - mu = 16 N-s

⇒ m(v-u) = 16 N-s

⇒ v - u =
`(16)/(m)`

=
`(16)/(2)\ m/s`

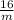
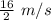
= 8 m/s

⇒ v = u + 8 m/s

= 3.0 m/s + 8.0 m/s

= 11 m/s [ans]