Question

Determine if it has a minimum of maximum and what that value is whilst also Identifying the domain and range

Answer 1

Hello!

First, let's rewrite the expression here:

`f\mleft(x\mright)=-2x^2+12x-15`

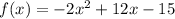
We will have to find the coefficients a, b and c:

• a ,= -2;

,

• b ,= 12;

,

• c ,= -15;

As we can see, coefficient a is negative. It means that the parabola will face downwards and have a maximum value.

We can obtain this point by using the two formulas below to calculate the coordinates (x, y) of this point, look:

`\begin{gathered} X_V=\text{ }-(b)/(2\cdot a) \\ \\ Y_V=-(b^2-4\cdot a\cdot c)/(4\cdot a) \end{gathered}`

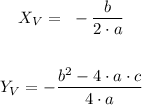
As we know the coefficients, let's replace the values in the formulas:

Xv:

`\begin{gathered} X_V=-(b)/(2\cdot a) \\ \\ X_V=-(12)/(2\cdot(-2))=-(12)/(-4)=-(-3)=+3 \\ \\ X_V=3 \end{gathered}`

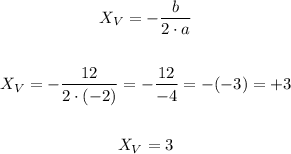
Now let's find Yv:

`\begin{gathered} Y_V=-(b^2-4\cdot a\cdot c)/(4\cdot a) \\ \\ Y_V=-(12^2-4\cdot(-2)\cdot(-15))/(4\cdot(-2))=-(144-120)/(-8)=-(24)/(-8)=-(-3)=+3 \\ \\ Y_V=3 \end{gathered}`

Doing this, we obtained the coordinate of the maximum point (x, y) = (3, 3).

As it doesn't have any restrictions, the domain will be: [-∞, +∞].

[tex]-\infty\: We have one restriction in the range, do you remember which?

The maximum value will be when y = 3, so the range is [-∞, 3].

Look at the graph of this function below: