Question

A ball is thrown in the air from a ledge. Its height in feet is represented by f(x) = –16(x2 – 7x – 8), where x is the number of seconds since the ball has been thrown. The height of the ball is 0 feet when it hits the ground. How many seconds does it take the ball to reach the ground?

Answer 1

`f(x)=-16( x^(2) -7x-8)`

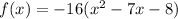
is the functions that determines the height of the ball in Feet, after x seconds being thrown.

so for example to calculate how many feet above the ground in the ball 5 seconds after being thrown, we calculate f(5)


`f(5)=-16( 5^(2) -7*5-8)=-16(25-35-8)=-16(-18)=288` feet

to solve our problem we need to find x such that f(x)=0

so we solve :


`-16( x^(2) -7x-8)=0`


`x^(2) -7x-8=0`

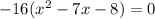
using the quadratic formula, le a=1, b=-7, c=-8


`√(D) = \sqrt{ b^(2)-4ac}= \sqrt{ (-7)^(2)-4(1)(-8) }= √(49+32)= √(81)=9`

so


`x_1= (-b+ √(D) )/(2a)= (7+9)/(2)= (16)/(2)=8`


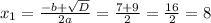
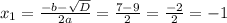
`x_1= (-b- √(D) )/(2a)= (7-9)/(2)= (-2)/(2)=-1`, which cannot be the solution to our problem.


Answer: 8 s