Question

The regular hexagon ABCDEF rotates 240º counterclockwise about its center to form hexagon A′B′C′D′E′F′. Point C′ of the image coincides with point __ of the preimage. Point D′ of the image coincides with point __ of the preimage.

Answer 1

The regular hexagon ABCDEF rotates 240º counterclockwise about its center to form hexagon A′B′C′D′E′F′. Point C′ of the image coincides with point _E_ of the preimage. Point D′ of the image coincides with point _F_ of the preimage.

Answer 2

Solution: The point C' of the image coincides with point E of the preimage and D' of the image coincide with the point F of the preimage.

Step-by-step explanation:

The regular hexagon have 6 corner points ABCDEF.

The complete angle about the center
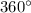`360^(\circ)`because it is a close figure as shown in given figure. It means the line from two consecutive vertices to the center of hexagon make an angle of
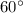`60^(\circ)` because 6 lines from the vertices to the center divides the center angle in 6 equal parts.

It is given that the hexagon is rotated at
`240^(\circ)` counterclockwise about the center, therefore the image of vertices shifts 4 places counterclockwise.

In figure first hexagon show preimage and second hexgon shows image. From figure it is noticed that the point C' of the image coincides with point E of the preimage and D' of the image coincide with the point F of the preimage.

Therefore, the point C' of the image coincides with point E of the preimage and D' of the image coincide with the point F of the preimage.