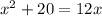Answer:
2 and 10 are solutions of given expression
Explanation:
Given expression
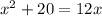
We have to find the values that are solutions of given expression.
Since, the given expression is a quadratic equation , thus the roots are the solutions of given expression.
Consider the given expression ,
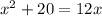
It can be written as ,
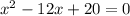
We can solve the given quadratic equation using middle term splitting method,
-12x can be written as -2x - 10x
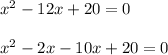
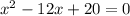
taking x common from first two terms and -10 common from last two terms, we have,
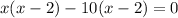
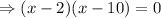
using zero product property, we have,
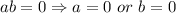
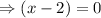 or
or
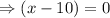
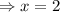 or
or
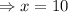
Thus, 2 and 10 are solutions of given expression