Question

Going against the current, a boat takes 6 hours to make a 120-mile trip. When the boat travels with the current on the return trip, it takes 5 hours. If x = the rate of the boat in still water and y = the rate of the current, which of the following systems could be used to solve the problem? 6(x - y) = 120 and 5(x + y) = 120 6(x + y) = 120 and 5(x - y) = 120 6x - 5y = 120 and x + y = 120

Answer 1

Answer: 6(x - y) = 120 and 5(x + y) = 120

Explanation:

Here x represents the rate of boat in still water and y represents the rate of stream,

Hence, the speed of boat with the current = x + y miles per hour

And, the speed of boat against the current = x - y miles per hour

Going against the current, a boat takes 6 hours to make a 120-mile trip.

⇒
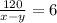`(120)/(x-y) = 6` ( Time = distance/ speed )

⇒
`120 = 6(x-y)`

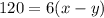
Again, When the boat travels with the current on the return trip, it takes 5 hours,

⇒
`(120)/(x+y) = 5`

⇒
`120 = 5(x+y)`

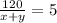
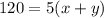
Therefore, first option is correct.

Answer 2

the formula would be 5(x+y) = 6(x-y) = 120

so 5(x+y)= 120 and 6(x-y)=120 can be used