Given that a small ball is fastened to a long rubber band and twirled around it such a way that the ball moves in an elliptical path given by the equation

,
where b and

are positive constants.
a) The velocity of the ball v as a function of time t is given by
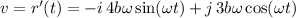
.
b) The speed of the ball v = |v| as a function of t is given by

.
c) The speed v at t = 0 at which time the ball is at its maximum distance from the origin is given by
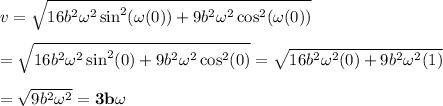
.
d) The speed v at
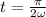
at which time the ball is at its minimum distance from the origin is given by
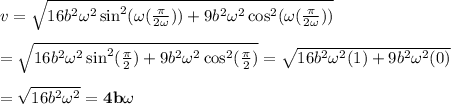
.
e) The acceleration of the ball, a, as a function of t is given by

.
f) The magnitude of the acceleration of the ball
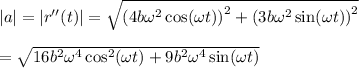
.