in Example #2,
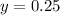 or
or
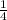 when rounded to the nearest hundredth.
when rounded to the nearest hundredth.
in Example #1,
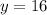 .
.
Here are the detailed steps to solve the proportions for
 :
:
Example #1:
The proportion is given by:
![\[ (4)/(9) = (y)/(36) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/oxo21ymgkzs5aofrttsx.png)
To solve for
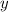 , cross-multiply to get:
, cross-multiply to get:
![\[ 4 * 36 = 9 * y \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2ax0hxkc7zcgjlucvstd.png)
![\[ 144 = 9y \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2un7wycf761pgl21dxw6.png)
Now, divide both sides by 9 to isolate
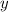 :
:
![\[ y = (144)/(9) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/oaewgen2bef41mjdbetk.png)
![\[ y = 16 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/wvnwv2mkd8ds51o5623q.png)
So, in Example #1,
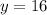 .
.
**Example #2:**
The proportion is given by:
![\[ (72)/(1.5) = (12)/(y) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/q0y73xg63wccl7no5obo.png)
To solve for
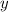 , cross-multiply to get:
, cross-multiply to get:
![\[ 72 * y = 12 * 1.5 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/28dzdgxz5bu83uxl1a4y.png)
![\[ 72y = 18 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/uf00xby7wxveeapj45ko.png)
Now, divide both sides by 72 to isolate
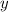 :
:
![\[ y = (18)/(72) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/3csosarqtg5jownhrxpt.png)
![\[ y = 0.25 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2zro6zf9tf2fejpu0dn7.png)
So, in Example #2,
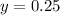 or
or
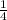 when rounded to the nearest hundredth.
when rounded to the nearest hundredth.