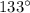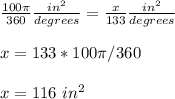Answer:
The answer is the option D
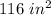
Explanation:
we know that
The area of a circle is equal to
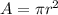
where
r is the radius of the circle
In this problem we have
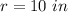
Substitute
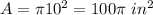
Remember that
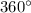 subtends the area of the complete circle
subtends the area of the complete circle
so
by proportion
Find the area of the shaded sector for an angle of