Question

The length of a rectangle is 2 more than 3 times the width. If the perimeter is 100 meters, what is the width of the rectangle?

Answer 1

So lets say the width of the rectangle is "x". This would make the length "3x+2".

The perimeter formula of a rectangle is P=2Length + 2width, so applying that to the problem:

100=2(x) + 2(3x+2)

Solving for x would give you x=12.

Since x is the width, the answer would be 12.

I hope this helps!

Answer 2

Answer: The required width of the given rectangle is 12 meters.

Step-by-step explanation: Given that the length of a rectangle is 2 more than three times the width and the perimeter is 100 meters.

We are to find the width of the rectangle.

Let w meters represents the width of the given rectangle.

Then, the length of the rectangle will be (3w + 2) meters.

According to the given information, we have

`Perimeter=100\\\\\Rightarrow 2\{(3w+2)+w\}=100\\\\\Rightarrow 2(3w+2+w)=100\\\\\Rightarrow 4w+2=50\\\\\Rightarrow 4w=50-2\\\\\Rightarrow 4w=48\\\\\Rightarrow w=(48)/(4)\\\\\Rightarrow w=12.`

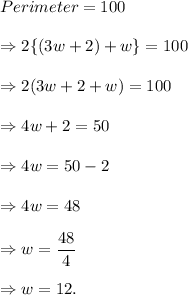
Thus, the required width of the given rectangle is 12 meters.