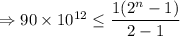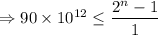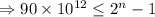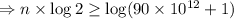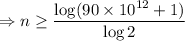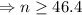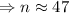Question

A leprechaun places a magic penny under a girls pillow. The next night there are 2 magic pennies under her pillow. The following morning she finds four pennies. Apparently, while she sleeps each penny turns into two magic pennies.The total number of pennies seen under the pillow each day is the grand total; that is, the pennies from each of the previous days are not being stored away until more pennies magically appear. How many days would elapse before she has a total of more than 90 trillion?

Answer 1

To determine when the girl has more than 90 trillion magic pennies due to exponential doubling each night, we solve for n in the inequality 2n > 90 trillion by taking the base 2 logarithm. We then round up to the next whole number to get the total number of days.

Step-by-step explanation:

The situation described where the magic penny doubles each night is an example of an exponential growth problem, specifically geometric progression. The number of pennies doubles each day, meaning we have 2n pennies on the nth day. To find out after how many days the girl has more than 90 trillion pennies, we need to solve the inequality 2n > 90 trillion.

The steps to solve the problem involve finding the logarithm base 2 of 90 trillion to get the value of n. Let's call 90 trillion T for simplicity:

1. Write the inequality as 2n > T.
2. Take the base 2 logarithm of both sides: log2(2n) > log2(T).
3. Simplify to find n: n > log2(T).
4. Use a calculator to find log2(T) and round up to the next whole number since we can't have a fraction of a day.

Once you calculate the exact number, you will have the number of nights required to exceed 90 trillion pennies.

Answer 2

After 47 days she will have more than 90 trillion pennies.

Step-by-step explanation:

At the beginning there was 1 penny. At the second day the amount of pennies under the pillow became 2.

The amount of pennies doubled each day. So the series is,

`1,2,4,8,16,32,.....`

This series is in geometric progression.

As the pennies from each of the previous days are not being stored away until more pennies magically appear so the sum of series will be,

`S_n=(a(r^n-1))/(r-1)`

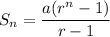
where,

a = initial term = 1,

r = common ratio = 2,

As we have find the number of days that would elapse before she has a total of more than 90 trillion, so

`\Rightarrow 90* 10^(12)\le (1(2^n-1))/(2-1)`

`\Rightarrow 90* 10^(12)\le (2^n-1)/(1)`

`\Rightarrow 90* 10^(12)\le 2^n-1`

`\Rightarrow 2^n\ge 90* 10^(12)+1`

`\Rightarrow \log 2^n\ge \log (90* 10^(12)+1)`

`\Rightarrow n* \log 2\ge \log (90* 10^(12)+1)`

`\Rightarrow n \ge (\log (90* 10^(12)+1))/(\log 2)`

`\Rightarrow n \ge 46.4`

`\Rightarrow n\approx 47`