cos 3x can be written using the sum and difference identity.
cos (3x) = cos (2x + 1)
cosx * cos2x - sinx * sin2x
next, you have to use the double angle identities for both sine and cosine. there are three options for cosine, so choose one. I'll use
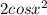
x - 1.
so, (
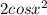
x - 1)cosx - 2sinx(cosxsinx)
you keep using those identities until you come to your final answer of
