Question

What is the factorization of the polynomial below?

3x2 + 33x + 54


A. 3(x + 2)(x + 9)

B. (x + 2)(x + 27)

C. (3x + 2)(x + 9)

D. (x + 3)(x + 9)

Answer 1

3x^2 + 33x + 54 =
3(x^2 + 11x + 18) =
3(x + 2)(x + 9) <==

Answer 2

A. 3(x+2)(x+9)

Explanation:

We have the expression
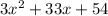`3x^2+33x+54`, we can rewrite the expression as:

`3x^2+33x+54=3.(1x^2)+3.(11x)+3.(18)`

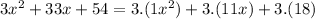
Then we can apply common factor 3:

`3.(1x^2)+3.(11x)+3.(18)=3(x^2+11x+18)`

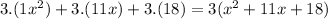
Now we are going to factor:
`x^2+11x+18`

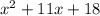
We can rewrite it as:
`x^2+2x+9x+18`, then we are going to use grouping, because we have 4 terms:

In

`x^2+2x=x.x+2.x=x(x+2)`

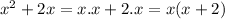
we use common factor x.

In

`9x+18=9.x+9.2=9(x+2)`

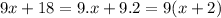
we use common factor 9.

Then we can express,

`x^2+11x+18=x(x+2)+9(x+2)\\=(x+9)(x+2)`

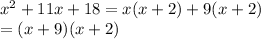
Now replacing:

`3(x^2+11x+18)=3(x+9)(x+2)=3(x+2)(x+9)`

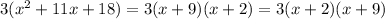
Then the correct answer is option A. 3(x+2)(x+9)