Question

If the following system of equations was written as a matrix equation in the form AX = C,? and matrix A was expressed in the form, a=[a c] [b d] find the value of a - b + c + d. 5x+7y=7 3x-2y=9

Answer 1

Answer is a - b + c + d = 7

Explanation:

The given equations are 5x + 7y = 7 and 3x - 2y = 9

Since system of equations are written in the form of AX = C

Now we will form the matrix form these equation.

A =
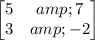
`\begin{bmatrix}5&7 \\ 3&-2 \end{bmatrix}`

X =
`\begin{bmatrix}x & y \end{bmatrix}`

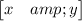
C =
`\begin{bmatrix}7 & 9\end{bmatrix}`

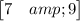
Since A =
`\begin{bmatrix}a & c\\ b & d\end{bmatrix}`

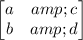
So a = 5, b = 3, c = 7 and d = -2

Now we can find the solution of ( a - b + c + d )

a - b + c + d = 5 - 3 + 7 - 2 = 2 + 5 = 7

So the answer is a - b + c + d = 7

Answer 2

The given equations are
5x + 7y = 7
3x - 2y = 9

As a matrix equation,
A = [5 7
3 -2]

X = [x
y]

C = [7
9]
That is
a =5, c=7; and b=3, d=-2

a - b + c + d = 5 - 3 + 7 + (-2) = 7

Answer: 7