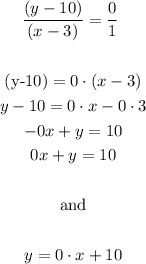We are told that the line passes through (3,10) and is parallel to y=-9, so, we have something like this:
So, we need to find the yellow line equation.
Standard form:
A straight line equation in standard form is something like this equation:
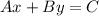
To do this, we can start for here:
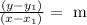
Where (x_1, y_1) is a point through which the line passes and m is the slope of the line.
In our case the point is (3,10) and the slope is 0 (since the line is parallel to y=-9):
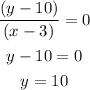
Slope-intercept form:
This equation is something like this:

Where m is, once again, the slope, and b is the y-intercept (the point where the line cross the y axis).
So, we have:

Answer