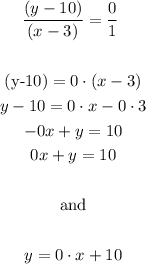Question

Write an equation (a) in standard form and (b) in slope-intercept form for the line described.through (3,10), parallel to y= -9

Answer 1

We are told that the line passes through (3,10) and is parallel to y=-9, so, we have something like this:

So, we need to find the yellow line equation.

Standard form:

A straight line equation in standard form is something like this equation:

`Ax+By=C`

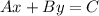
To do this, we can start for here:

`\frac{(y-y_1)}{(x-x_1)_{}}=\text{ m}`

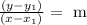
Where (x_1, y_1) is a point through which the line passes and m is the slope of the line.

In our case the point is (3,10) and the slope is 0 (since the line is parallel to y=-9):

`\begin{gathered} \frac{(y-10)}{(x-3)_{}}=0 \\ y-10=0 \\ y=10 \end{gathered}`

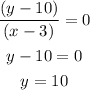
Slope-intercept form:

This equation is something like this:

`y=mx+b`

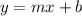
Where m is, once again, the slope, and b is the y-intercept (the point where the line cross the y axis).

So, we have:

`\begin{gathered} y=0\cdot x+10 \\ y=10 \end{gathered}`

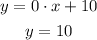
Answer

`\begin{gathered} \frac{(y-10)}{(x-3)_{}}=(0)/(1)\text{ } \\ \\ \text{(y-}10)=0\cdot(x-3) \\ y-10=0\cdot x-0\cdot3 \\ -0x+y=10 \\ 0x+y=10 \\ \\ \text{and} \\ \\ y=0\cdot x+10 \end{gathered}`