Question

Given circle X with radius 10 units and chord AB with length 12 units, what is the length of segment CX, which bisects the chord? A. 10 units B. 8 units C. 6 units D. 16 units

Answer 1

Consider the circle with center X, as shown in the figure.

Draw the diameter of the circle which is parallel to cherd AB, as shown in the figure.

Since the diameter and AB are parallel, then the line segment XC which bisects AB at C, will be perpendicular to AB.

SO triangle XCB is a right triangle. Thus the length of CX, by the Pythagorean theorem is


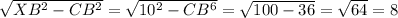
`\sqrt{ XB^(2)- CB^(2)} = \sqrt{ 10^(2)- CB^(6)}= √(100-36)= √(64)=8` units.


Answer: 8 units