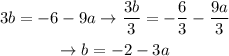How to clear an equation/solve for any given variable?
Lets say you have two identical cups of coffee, a and b.
You can say they're both equal. If you want to add a tablespoon of sugar to cup a, and you also want both cups to remain equal, you'll have to add the same tablespoon of sugar to cup b.
We use this fact, called conservation of an equality, to clear an equation (A.K.A solving for a variable)
Mathematically speaking,
Cups a and b are equal
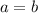
If you modify a, you'll have to modify b the same way
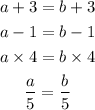
Now, let's apply that logic to the equation we have.
We know cup of coffee a is

And cup b is
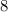
We also know both cups of coffee are equal, so
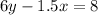
We're being asked to solve for y. In other words, we have to clear y from this expression.
Let's add our first tablespoon of sugar: adding 1.5x to both sides:
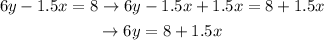
See how the -1.5x canceled out? That's what we're looking for! We want y to be left alone in its side.
Now, let's divide both sides by 6 to cancel out the 6 from 6y:
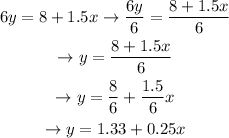
He have cleared y / solved the equation for y
Let's try with another example
e.g:
Solve the following equation for b

Solution: Let's substract 12 from both sides:
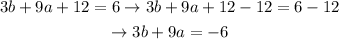
Then, let's substract 9a from both sides
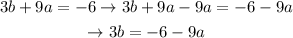
Let's divide both sides by 3