Question

Part A: Amir rented a scooter at $43 for 3 hours. If he rents the same scooter for 8 hours, he has to pay a total rent of $113. Write an equation in the standard form to represent the total rent (y) that Amir has to pay for renting the scooter for x hours.

Part B: Write the equation obtained in Part A using function notation.

Part C: Describe the steps to graph the equation obtained above on the coordinate axes. Mention the labels on the axes and the intervals.

Answer 1

PART A:
Recall that the equation of a line in standard form is of the form:
ax + by = c
where a, b, and c are constants.

The equation of a line passing through two points:

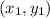
`(x_1,y_1)` and
`(x_2,y_2)`
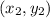
is given by:

`(y-y_1)/(x-x_1) = (y_2-y_1)/(x_2-x_1)`

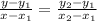
Given that Amir rented a scooter at $43 for 3 hours. If he rents the same scooter for 8 hours, he has to pay a total rent of $113.

Thus,

`(x_1,y_1)=(3,43)` and
`(x_2,y_2)=(8,113)`

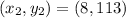
Thus, the equation of the line is given by:

`(y-43)/(x-3) = (113-43)/(8-3) = (70)/(5) =14 \\ \\ y-43=14(x-3)=14x-42 \\ \\ y=14x+1`

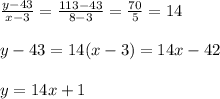
Therefore, the equation of the line in standard form is

`14x-y=-1`


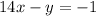
PART B:
To write the equation with a function notation, we first express y in terms of x and then change y notation to f(x) notation.

Recall from part 1:

`y=14x+1`

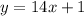
Therefore, the equation obtained in Part A written using function notation is given by:

`f(x)=14x+1`


PART C:
To graph the equation obtained above, we draw the x- and y- axis with the x-axis labelled 'number of hours' and the y-axis labelled 'total rent'.

Next, we choose appropriate scales for x- and y- axis. Depending on the size of your graph book, you can choose an interval of 1 unit for the x-axis and an interval of 10 units for the y-axis.

From part A, we know that the line of the equation passes though points (3, 43) and (8, 113), mark these points and draw a straight line passing theough these points.