Answer:
Given angle terminates in Quadrant 1.
Explanation:
We have to tell in which quadrant Angle
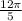 lies
lies
First we simply the given angle,
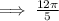

we know that
2π represent one complete revolution.
⇒
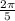 decides given angles belongs to which quadrant.
decides given angles belongs to which quadrant.
Value of
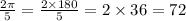
So,
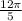 lie in 1st Quadrant as 72 lies in 1st quadrant
lie in 1st Quadrant as 72 lies in 1st quadrant
Therefore, Given angle terminates in Quadrant 1.