Answer: The missing reason in Step 7 is ' Consecutive interior angles add up to 180°'
Step-by-step explanation:
Since we know that, The sum of two consecutive interior angles made by same transversal on two parallel lines is always equal to 180°.
And, here
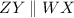 and XY is the common transversal, Also, ∠WYX and ∠WXY are the consecutive angles on lines ZY and WX respectively by transversal YX. ( shown on figure)
and XY is the common transversal, Also, ∠WYX and ∠WXY are the consecutive angles on lines ZY and WX respectively by transversal YX. ( shown on figure)
Therefore, m∠ZYX + m∠WXY = 180°
Here, Given, WXYZ is a parallelogram in which
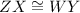
we have to prove that: WXYZ is a rectangle.
Statement Reason
1. WXYZ is a parallelogram, 1. Given
ZX ≅WY
2. ZY ≅ WX 2. opposite sides of parallelogram
are congruent.
3. YX≅YX 3. Reflexive
4. ΔZYX ≅ Δ WXY 4. SSS postulate of congruence
5. ∠ZYX ≅ ∠WXY 5. CPCTC
6. m∠ZYX ≅ m∠WXY 6. definition of congruence.
7.m∠ZYX + m∠WXY = 180° 7.Consecutive interior
angles add up to 180°'
8.m∠ZYX + m∠ZYX = 180° 8. By substitution
9. 2(m∠ZYX) = 180° 9. By simplification
10.m∠ZYX = 90° 10.division property of equality
11. WXYZ is a rectangle 11.Rectangle angle theorem.