Question

Suppose A and B are dependent events. If P(A|B)=0.55 and P(B)=0.2 , what is P(AuB) ?

Answer 1

Hence,

P(A∪B)=0.89

Explanation:

As we are given that:

A and B are dependent events.

If P(A|B)=0.55 and P(B)=0.2 .

AS we know that:

P(A)+P(B)=1

⇒ P(A)+0.2=1

⇒ P(A)=1-0.2

⇒ P(A)=0.8.

Also we know that:

`P(A|B)=(P(A\bigcap B))/(P(B))\\\\\\i.e.\\\\0.55=(P(A\bigcap B))/(0.2)\\\\P(A\bigcap B)=0.55* 0.2\\\\P(A\bigcap B)=0.11`

Hence,

`P(A\bigcup B)=P(A)+P(B)-P(A\bigcap B)\\\\P(A\bigcup B)=0.8+0.2-0.11\\\\P(A\bigcup B)=0.89`

Hence,

P(A∪B)=0.89

Answer 2

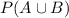`P(A \cup B)` = 0.89

Explanation:

Using the formula:

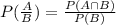`P((A)/(B)) = (P(A \cap B))/(P(B))` ....[1]

where, A and B are events.

As per the statement:

Suppose A and B are dependent events.

If
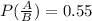`P((A)/(B))=0.55` and P(B) = 0.2

Substitute these in [1] we get;

`0.55 = (P(A \cap B))/(0.2)`

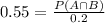
Multiply both sides by 0.2 we have;

`0.11 = P(A \cap B)`

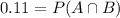
We know that:

`P(A)+P(B) = 1`

⇒
`P(A) = 1-P(B)`

⇒
`P(A) = 1-0.2 = 0.8`

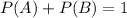
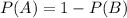
We have to find
`P(A \cup B)`

`P(A \cup B) = P(A)+P(B) -P(A \cap B)`

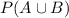
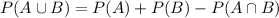
Substitute the given values we have;

`P(A \cup B) = 0.8+0.2-0.11 = 1.0-0.11 = 0.89`

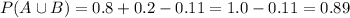
Therefore, the value of
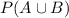`P(A \cup B)` is, 0.89