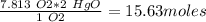Question

Mercury(II) oxide (HgO) decomposes to form mercury (Hg) and oxygen (O2). The balanced chemical equation is shown below. 2HgO mc020-1.jpg 2Hg + O2 The molar mass of HgO is 216.59 g/mol. The molar mass of O2 is 32.00 g/mol. How many moles of HgO are needed to produce 250.0 g of O2?

Answer 1

2HgO = 2Hg + O₂

n(HgO)=2n(O₂)=2m(O₂)/M(O₂)

m(HgO)=n(HgO)M(HgO)=2m(O₂)M(HgO)/M(O₂)

m(HgO)=2*250.0*216.59/32.00 = 3384.219 g ≈ 3 kg 384 g

Answer 2

moles of HgO needed to produce 250.0 g of O2 = 15.63 moles

Step-by-step explanation:

The chemical reaction is:

`2HgO\rightarrow 2Hg + O2`

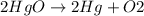
Amount of O2 produced = 250.0 g

Molar mass of HgO = 216.59 g/mol

Molar mass of O2 = 32.00 g/mol

Moles of O2 produced =
`(Mass\ of\ O2)/(Molar\ Mass) = (250.0g)/(32 g/mol ) = 7.813 moles`

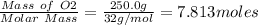
Based on the reaction stoichiometry:

2 moles of HgO produces 1 mole of O2

Therefore, moles of HgO needed to produce 7.813 moles of O2 is:

=
`(7.813\ O2 * 2\ HgO)/(1\ O2) = 15.63 moles`