Question

Diana works in a building that is 130 feet tall. She is outside, looking up at the building at an angle of 37° from her feet to the top of the building. 

If Diana walks forward and her angle looking to the top of the building changes to 40°, how much closer is she to the building? Round the answer to the nearest tenth of a foot.
10.3 ft
17.6 ft
30.2 ft
97.2 ft

Answer 1

Let x be her initial distance from the building, then tan 37 = 130/x
x = 130/tan 37 = 130/0.7536 = 172.5 feet

Let y be her distance from the building after moving forward, then
tan 40 = 130/y
y = 130/tan 40 = 130/0.8391 = 154.9

After moving forward, she is 172.5 - 154.9 = 17.6 ft closer.

Answer 2

17.6ft

Explanation:

Givens

• The building is 130 feet tall.
• The angle we between the view line from her eyes and the ground is 37°.
• The second angle between her view line and the ground is 40°.

If we draw the situation, it would be like the one presented in the image attached.

To find the answer, we need to find the distance when the angle is 37° and the distance when the angle is 40°, to do so, we have to use the trigonometric reasons.

In this case, we have the angle and its opposite leg. In order to find the horizontal distance, we need to use the tangent

`tan37\° = (130ft)/(d_(1) )\\d_(1)=(130ft)/(0,753554) \approx 172.5 ft`

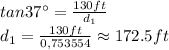
Then, the angle changes to 40°, but the height of the building remains the same obsviously

`tan40\° = (130ft)/(d_(1) )\\d_(1)=(130ft)/(0,839099) \approx 154. 9ft`

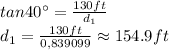
Now, we need to find the difference,

`d=d_(1) -d_(2) =172.5ft - 154.9ft=17.6ft`

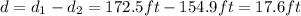
Therefore, the right answer is 17.6ft, the second choice.