Question

Solve the following system of equations 2x+7y=-1 4x-37=-19

Answer 1

2x + 7y = -1 .....multiply by -2
4x - 3y = -19
---------------
-4x - 14y = 2...(result of multiplying by -2)
4x - 3y = -19
---------------add
-17y = -17
y = -17/-17
y = 1

2x + 7y = -1
2x + 7(1) = -1
2x + 7 = -1
2x = -1 - 7
2x = - 8
x = -8/2
x = -4

solution is (-4,1)

Answer 2

Answer: The required solution of the given system is

x = -4 and y = 1.

Step-by-step explanation: We are given to solve the following system of linear equations :

`2x+7y=-1~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)\\\\4x-3y=-19~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

We will be using the method of Elimination to solve the given system.

Multiplying equation (i) by 2, we have

`2(2x+7y)=-1*2\\\\\Rightarrow 4x+14y=-2~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(iii)`

Subtracting equation (i) from equation (iii), we get

`(4x+14y)-(4x-3y)=-2-(-19)\\\\\Rightarrow 17y=-2+19\\\\\Rightarrow 17y=17\\\\\Rightarrow y=(17)/(17)\\\\\rightarrow y=1.`

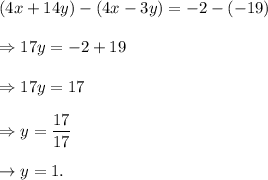
Substituting the value of y in equation (i), we get

`2x+7*1=-1\\\\\Rightarrow 2x+7=-1\\\\\Rightarrow 2x=-1-7\\\\\Rightarrow 2x=-8\\\\\Rightarrow x=-(8)/(2)\\\\\Rightarrow x=-4.`

Thus, the required solution of the given system is

x = -4 and y = 1.